위상정렬이란?
DAG(Directed Acyclic Graph, 방향이 있고 사이클이 없는 그래프)에서 방향을 거스르지 않고 나열하는 것을 위상정렬이라고 한다.
예를 들어

이 그래프에서 위상정렬을 하면 1->2->4->3 또는 1->2->3->4가 결과로 나올 수 있다.(위상정렬의 결과는 여러가지일 수 있다.)
DFS를 이용한 구현
dfs를 수행하며 방문한 정점의 순서를 구하면 된다.
dfs를 수행하며 dfs가 종료되는 순서를 기록한 후 이를 뒤집어주면 된다.
방문하는 정점들을 스택에 집어넣고 차례대로 꺼내면서 출력해줘도 된다.
아래 코드는 방문한 정점들을 벡터에 집어넣고 벡터를 뒤집었다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, m;
bool visited[1001];
vector<int> adj[1001];
vector<int> ans;
void dfs(int x)
{
if(visited[x]){ return; }
visited[x]=1;
for(int nxt : adj[x]){
if(visited[nxt]==0){
dfs(nxt);
}
}
ans.push_back(x);
}
int main()
{
cin >> n >> m;
for(int i=1; i<=m; i++){
int a, b;
cin >> a >> b;
adj[a].push_back(b);
}
dfs(1);
reverse(ans.begin(), ans.end());
for(int i=0; i<ans.size(); i++){
cout << ans[i] << " ";
}
return 0;
}
BFS를 이용한 구현
이 방법은 들어오는 간선의 개수를 이용하여 위상정렬을 하는 방법이다.
정점 $u$로 들어오는 간선의 개수를 $indegree[u]$라고 할 때
$1.$ $indegree$가 $0$인 정점을 모두 큐에 넣는다. $indegree$가 0이라는 것은 이 정점으로 들어오는 간선이 하나도 없다는 뜻이기 때문에 이 정점을 방문하기 전에 먼저 방문해야하는 정점이 없거나, 아니면 이미 방문했다는 뜻이다.
$2.$ 정점의 개수만큼 반복: 큐의 맨 앞의 원소를 제거해서 이 정점에서 나가는 모든 간선을 지운다. 이 때 $indegree$가 $0$이 된 정점을 모두 큐에 넣는다.
$3.$ 이 때 큐에서 빼는 정점의 순서가 위상 정렬의 순서이다.
이 때 $2.$에서 나가는 간선을 지우는 방법은 그냥 인접한 정점의 $indegree$를 1씩 감소시키면 된다.
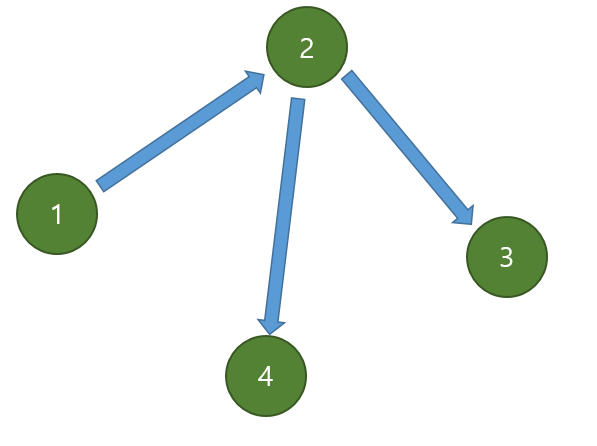
위에서 봤던 그래프에서 $indegree$가 $1$번 정점은 0, $2$번 정점은 1, $3$번 정점은 1, $4$번 정점은 1이므로
$1$번 정점을 큐에 넣는다.
$1$번에서 나가는 간선을 모두 지우면 $2$번 정점도 $indegree$가 0이 되므로 $2$번 정점을 큐에 넣는다.
이런 식으로 계속 하면 위상정렬을 할 수 있다.
이 때 정점을 모두 방문하기 전에 큐가 비어버리면 이건 위상정렬이 안되는 그래프, 즉 사이클이 있다는 의미이다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int n, m;
int indegree[1001];
bool visited[1001];
vector<int> adj[1001];
vector<int> ans;
queue<int> q;
int main()
{
cin >> n >> m;
for(int i=1; i<=m; i++){
int a, b;
cin >> a >> b;
adj[a].push_back(b);
indegree[b]++;
}
for(int i=1; i<=n; i++){
if(indegree[i]==0){ q.push(i); }
}
for(int i=1; i<=n; i++){
if(q.empty()){
cout << -1 << "\n"; //위상정렬 불가능
return 0;
}
int x=q.front();
q.pop();
ans.push_back(x);
for(int nxt : adj[x]){
indegree[nxt]--;
if(indegree[nxt]==0){ q.push(nxt); }
}
}
for(int i=0; i<ans.size(); i++){
cout << ans[i] << " ";
}
return 0;
}
연습
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int N, M;
vector<int> adj[32001];
int indegree[32001];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> N >> M;
for(int i=1; i<=M; i++){
int a, b; cin >> a >> b;
adj[a].push_back(b);
indegree[b]++;
}
queue<int> q;
for(int i=1; i<=N; i++){
if(indegree[i]==0){
q.push(i);
}
}
for(int i=1; i<=N; i++){
int x=q.front();
q.pop();
cout << x << " ";
for(int nxt : adj[x]){
indegree[nxt]--;
if(indegree[nxt]==0){
q.push(nxt);
}
}
}
return 0;
}
BOJ 3665 최종 순위: 작년의 순위가 입력으로 주어지고 순위의 변경이 주어질 때, 올해의 순위를 구하는 문제이다. 여기서 순위의 변경 (a, b)의 입력은 a가 b보다 앞서는 순위로 바뀌었다는 뜻이 아니고 a와 b의 상대적인 순위를 바꾼다는 표현임에 주의해야한다. 먼저 N의 크기가 작기 때문에 2차원 배열로 인접 행렬을 만들어준다. 2차원 배열 a[x][y]에서 x가 y보다 앞선 순위라면 1, 그렇지 않으면 0으로 해주고, bfs를 이용한 위상정렬을 하면 된다.
#include <iostream>
#include <vector>
#include <queue>
#include <memory.h>
using namespace std;
typedef long long ll;
int n, m;
int win[501][501];
int a[501];
int indegree[501];
void solve()
{
memset(win, 0, sizeof(win));
scanf("%d", &n);
for(int i=1; i<=n; i++){
scanf("%d", &a[i]);
indegree[i]=0;
}
for(int i=1; i<=n; i++){
for(int j=i+1; j<=n; j++){
win[a[i]][a[j]]=1;
indegree[a[j]]++;
}
}
scanf("%d", &m);
while(m--){
int x, y;
scanf("%d %d", &x, &y);
if(win[y][x]==1){
win[y][x]=0;
win[x][y]=1;
indegree[x]--; indegree[y]++;
}
else if(win[x][y]==1){
win[x][y]=0;
win[y][x]=1;
indegree[y]--; indegree[x]++;
}
}
queue<int> q;
for(int i=1; i<=n; i++){
if(indegree[i]==0){
q.push(i);
}
}
vector<int> ans;
for(int k=1; k<=n; k++){
if(q.empty()){
printf("IMPOSSIBLE\n");
return;
}
int x=q.front(); q.pop();
ans.push_back(x);
for(int i=1; i<=n; i++){
if(win[x][i]){
indegree[i]--;
if(indegree[i]==0){
q.push(i);
}
}
}
}
for(int i : ans){
printf("%d ", i);
}
printf("\n");
}
int main()
{
int t;
scanf("%d", &t);
while(t--){
solve();
}
return 0;
}'Algorithm' 카테고리의 다른 글
| 벨만 포드 알고리즘(Bellman Ford Algorithm) (0) | 2021.02.14 |
|---|---|
| 최소 공통 조상(LCA) 알고리즘 (0) | 2021.02.11 |
| 투 포인터(Two Pointer) (0) | 2021.02.11 |
| 동적계획법(경로 역추적) (0) | 2021.02.11 |
| Algorithm이란? (0) | 2021.02.11 |