투 포인터란?
배열 내에서 연속된 값들을 이용해서 문제를 해결해야할 때, 두 개의 인덱스를 나타내는 변수들을 움직이며 문제를 해결하는 알고리즘이다.
예를 들어 $N$개의 자연수로 이루어진 수열이 주어졌을 때, 이 수열에서 연속되는 부분 수열 중 합이 $S$가 되는 부분 수열의 개수를 구하는 알고리즘을 생각해보자.
- $O(N^{2})$의 알고리즘
연속된 부분 수열 중 합이 S인 부분 수열의 개수를 찾아야 한다. 부분 수열의 시작 인덱스와 끝 인덱스를 각각 a, b라고 하면 가능한 모든 (a, b)의 순서쌍을 구하고 각각의 부분 수열이 합이 S가 되는지를 확인하면 된다.
예를 들어 [5, 4, 3, 2, 6, 3, 5, 9, 10]의 수열에서 부분 수열 [4, 3, 2, 6, 3]은 1번 인덱스부터 5번 인덱스까지의 부분이므로 (a, b)=(1, 5)이다.
가능한 모든 (a, b)의 개수는 근사적으로 $N^{2}$개일 것이다. 따라서 이 때 시간복잡도는 $O(N^{2})$이다.
#include <iostream>
using namespace std;
int main()
{
int n, S, arr[100001];
scanf("%d %d", &n, &S);
for(int i=0; i<n; i++){
scanf("%d", &arr[i]);
}
int ans=0;
for(int a=0; a<n; a++){
int sum=0;
for(int b=a; b<n; b++){
sum+=v[b];
if(sum==S){ ans++; }
if(sum>S){ break; }
}
}
printf("%d\n", ans);
return 0;
}
하지만 수열의 길이가 $100,000$ 정도라면 이 방법으로는 1초 내에 풀 수가 없다.
- 2. 투 포인터를 이용한 $O(N)$ 구현
투 포인터 알고리즘을 사용하는데, 위와 같이 부분 수열의 시작점과 끝점 인덱스를 나타내는 순서쌍을 이용할 것이다. 그 순서쌍을 (s, e)라고 하자.
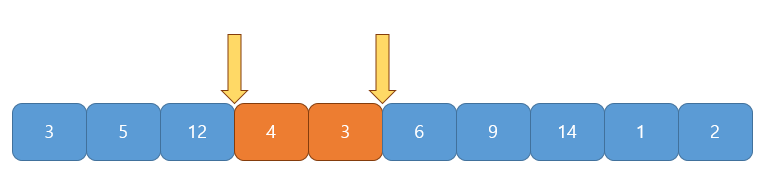
예시로 어떤 수열의 구성이 $[ 3, 5, 12, 4, 3, 6, 9, 14, 1, 2 ]$이고 $S$가 $14$라고 가정하자.
s, e는 0부터 시작해서 아래와 같은 연산을 반복한다.
- 부분 수열의 합이 $S$보다 작다면 e 1증가
- 부분 수열의 합이 $S$보다 크거나 같다면 s 1증가
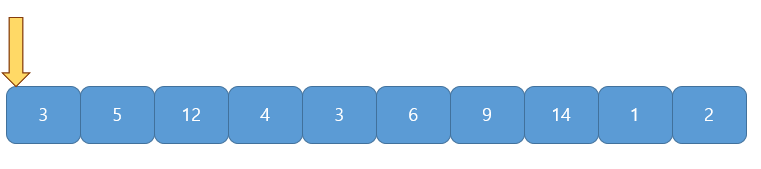
부분합이 $0$으로 $S$보다 작으므로 e가 1 증가

부분합이 $3$으로 $S$보다 작으므로 e가 1 증가

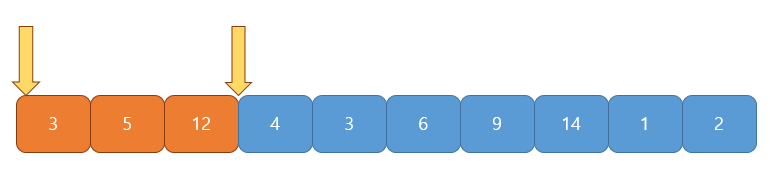
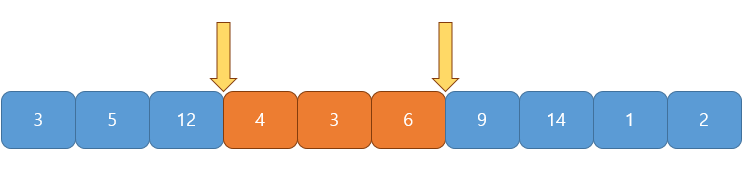
부분합이 $20$으로 $S$보다 크므로 s가 1 증가

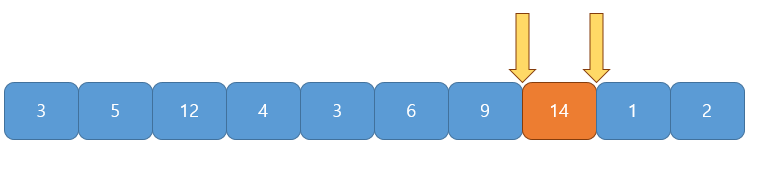
부분합이 $17$로 $S$보다 크므로 $s$ $1$증가
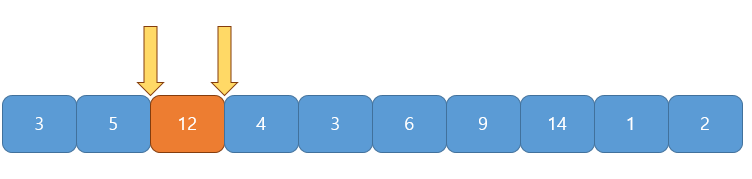

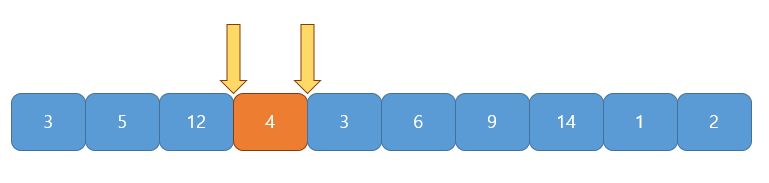







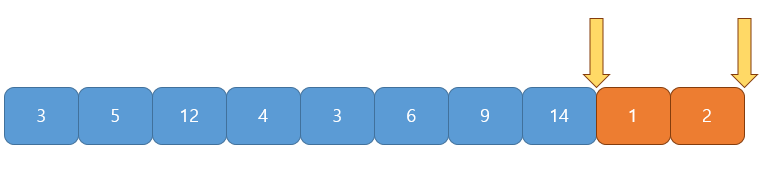
이 과정을 끝의 인덱스에 도달할 때까지 반복하면 시간복잡도 O(N)에 문제를 해결할 수 있다.
#include <iostream>
using namespace std;
int n, S, arr[100001];
int main()
{
scanf("%d %d", &n, &S);
for(int i=0; i<n; i++){
scanf("%d", &arr[i]);
}
int s=0, e=0, ans=0;
int sum=0;
while(1){
if(sum>=S) sum-=arr[s++];
else if(e==n) break;
else sum+=v[e++];
if(sum==S) ans++;
}
printf("%d\n", ans);
return 0;
}
'Algorithm' 카테고리의 다른 글
| 최소 공통 조상(LCA) 알고리즘 (0) | 2021.02.11 |
|---|---|
| 위상정렬(Topological Sort) (0) | 2021.02.11 |
| 동적계획법(경로 역추적) (0) | 2021.02.11 |
| Algorithm이란? (0) | 2021.02.11 |
| 세그먼트 트리(Segment Tree) (0) | 2021.02.11 |