Breadth-First-Search
DFS에서는 재귀 기반의 탐색 방법을 이용하여 그래프를 분기 별로 탐색했다. BFS는 Queue 기반의 탐색 방법으로, 모든 분기를 일정한 간격으로 탐색하는 방법이다. 즉, 분기가 n개 있다면 1번 분기에서 1개의 노드만큼 탐색하면 그 다음에는 2번 분기에서 1개의 노드만큼, ...을 반복하는 것이다. 다르게 표현하면 임의의 노드에서 시작하여 인접한 노드를 따라 모든 방향으로 조금씩 탐색을 진행한다. 구현은 Array를 이용해서도 가능하지만 선입선출(FIFO)의 Data Structure인 Queue를 이용하여 구현한다.
아래는 BFS가 Queue를 통해 어떻게 진행되는지 확인한다.
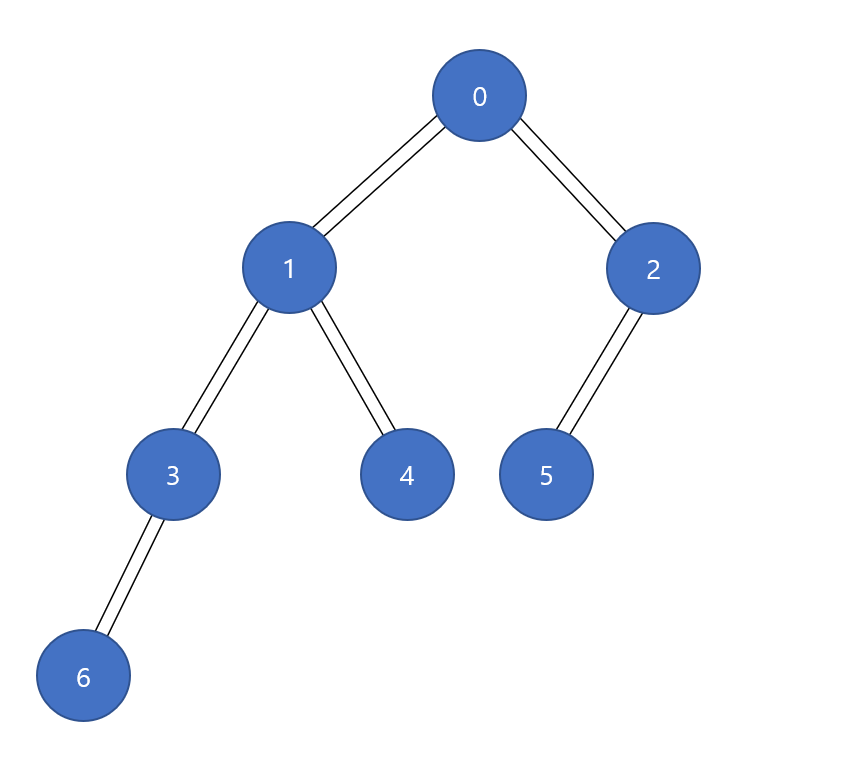
방문한 정점은 색을 주황색으로 표시하고, 0번부터 탐색을 시작할 것이다. 먼저 Queue에 시작 노드를 push한다.
queue에 0 push
------------------------------------------
queue - [0]
그리고 Queue의 front를 x라 하고, Queue를 pop한다. 이후, x와 인접한 노드를 Queue에 추가한다. 0번과 인접한 정점 중 방문하지 않은 1, 2번을 Queue에 넣는다.
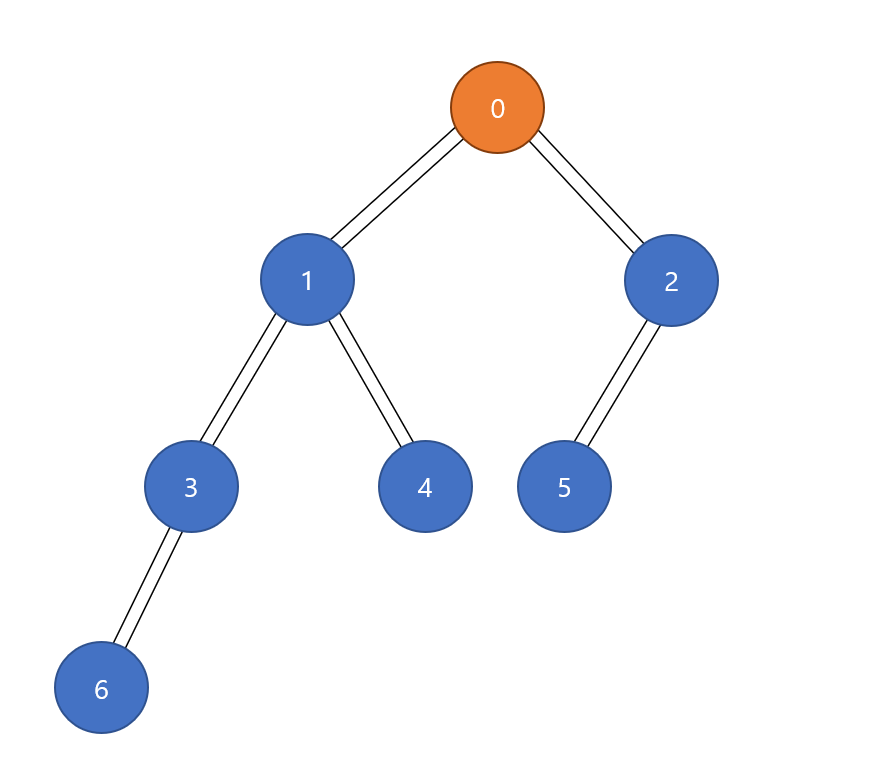
Queue의 front인 0번 pop
------------------------------------------
Queue - []
Queue에 1, 2번 push
------------------------------------------
Queue - [1, 2]
Queue의 front인 1번을 꺼내고, 1번과 인접한 정점 중 방문하지 않은 3, 4번을 Queue에 추가
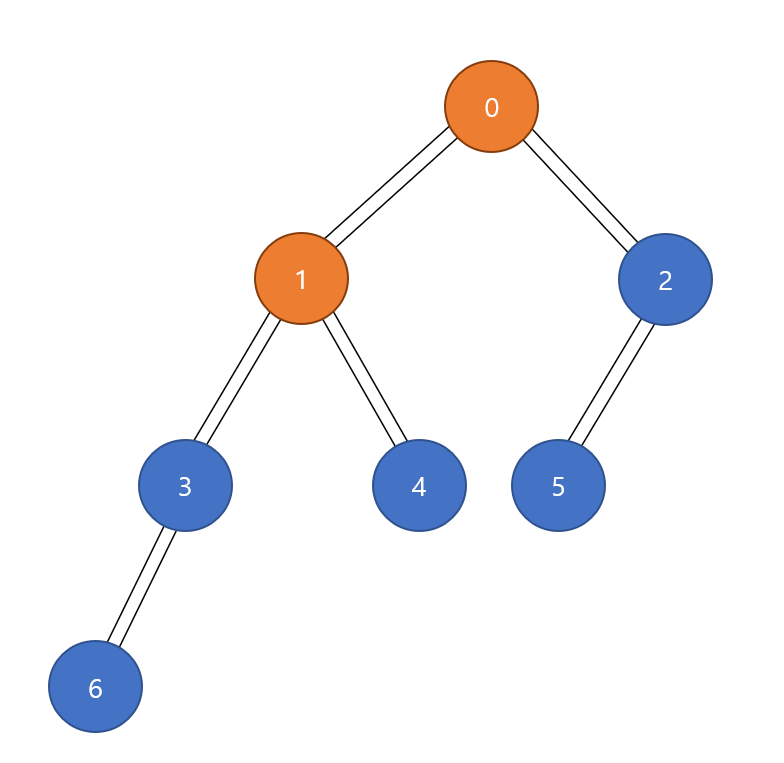
Queue의 front인 1번 pop
------------------------------------------
Queue - [2]
Queue에 3, 4번 push
------------------------------------------
Queue - [2, 3, 4]
Queue의 front인 2번을 꺼내고, 2번과 인접한 정점 중 방문하지 않은 5번을 Queue에 추가
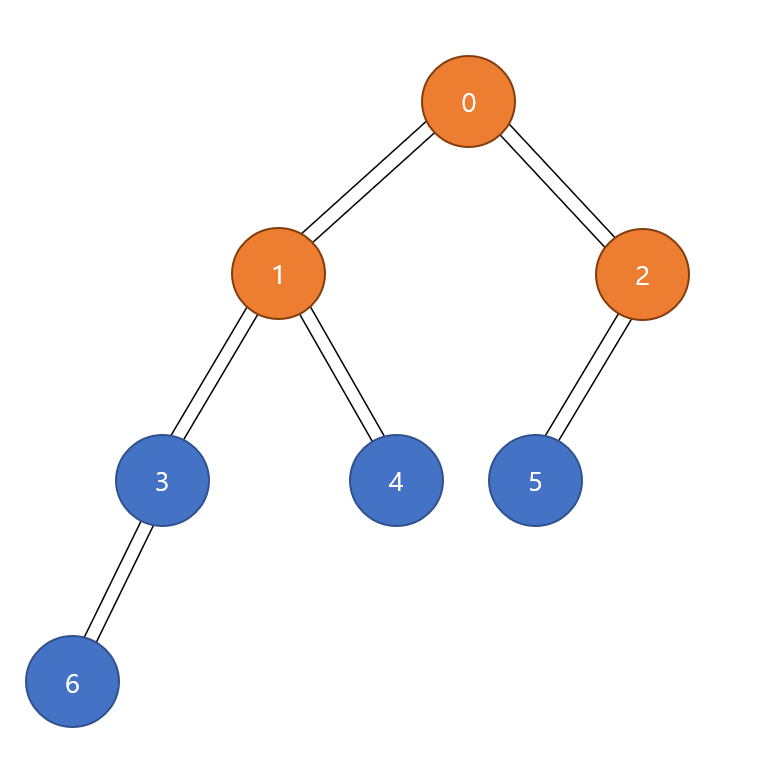
Queue의 front인 2번 pop
------------------------------------------
Queue - [3, 4]
Queue에 5번 push
------------------------------------------
Queue - [3, 4, 5]
Queue의 front인 3번을 꺼내고, 3번과 인접한 정점 중 방문하지 않은 6번을 Queue에 추가
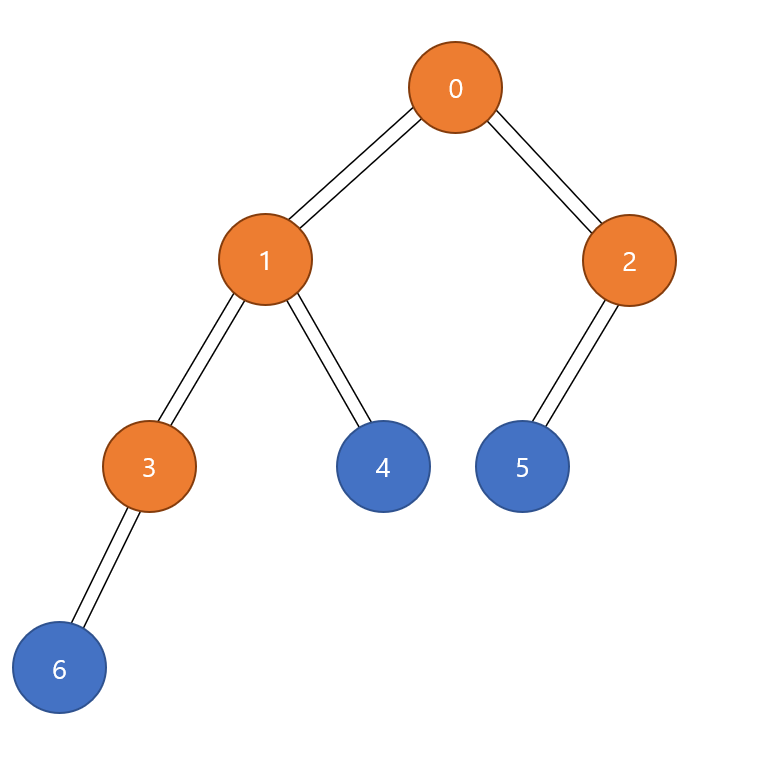
Queue의 front인 3번 pop
------------------------------------------
Queue - [4, 5]
Queue에 6번 push
------------------------------------------
Queue - [4, 5, 6]
Queue의 front인 4번 꺼내기, 4번과 인접한 정점 중 방문하지 않은 정점이 없으므로 Queue에 추가하지 않는다.
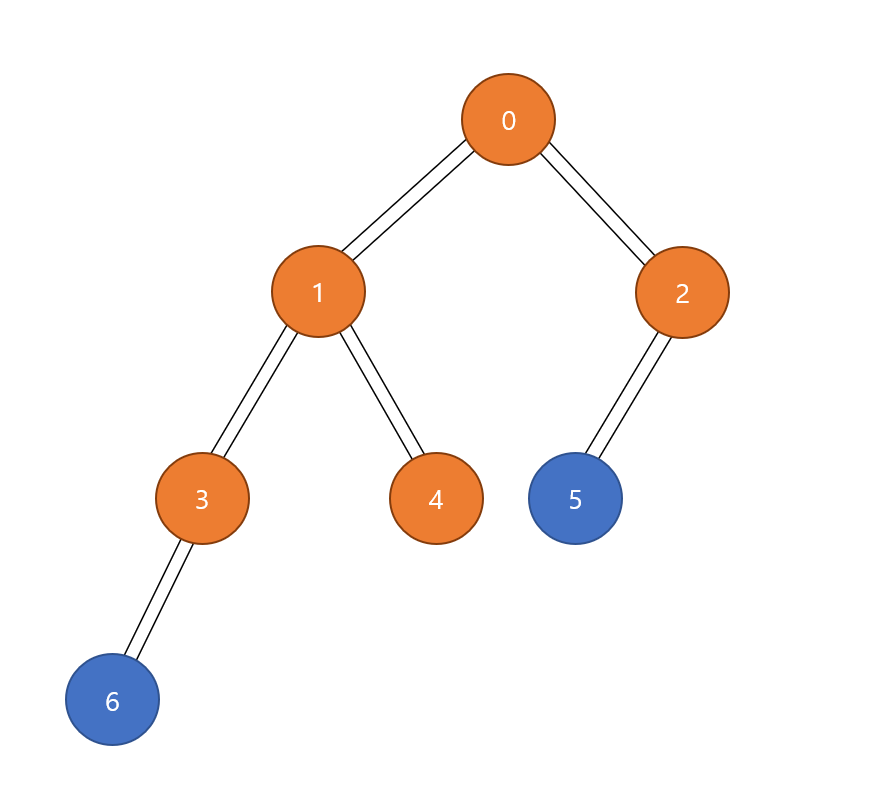
Queue의 front인 4번 pop
------------------------------------------
Queue - [5, 6]
Queue에 push하지 않음
Queue의 front인 5번 꺼내고, 5번과 인접한 정점 중 방문하지 않은 정점이 없으므로 Queue에 추가하지 않는다.
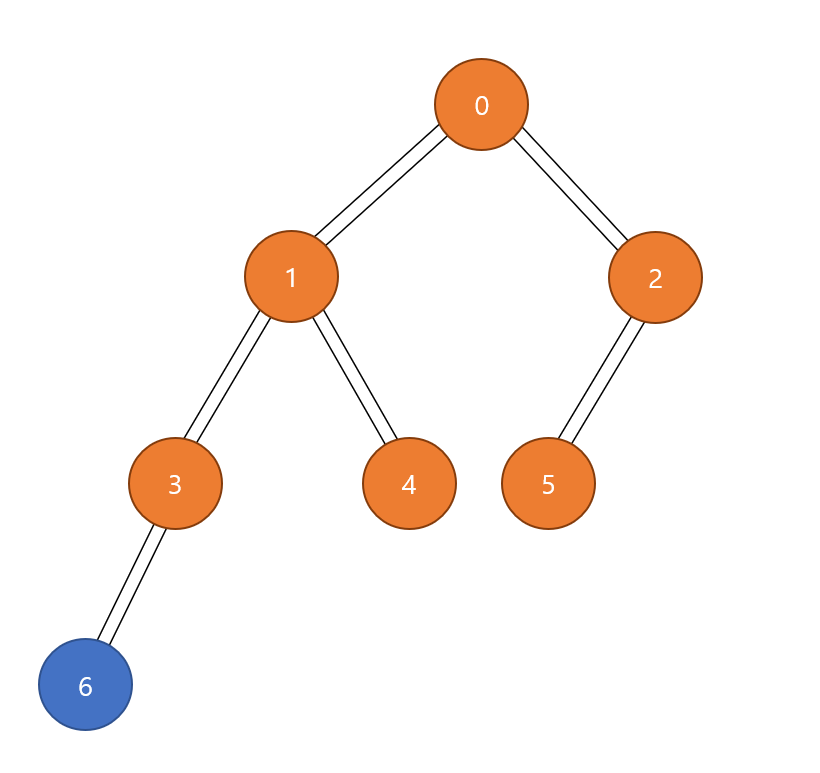
Queue의 front인 5번 pop
------------------------------------------
Queue - [6]
queue에 push하지 않음
Queue의 맨 앞에 있는 6번 방문, 6번과 인접한 정점 중 방문하지 않은 정점이 없으므로 queue에 추가하지 않는다.
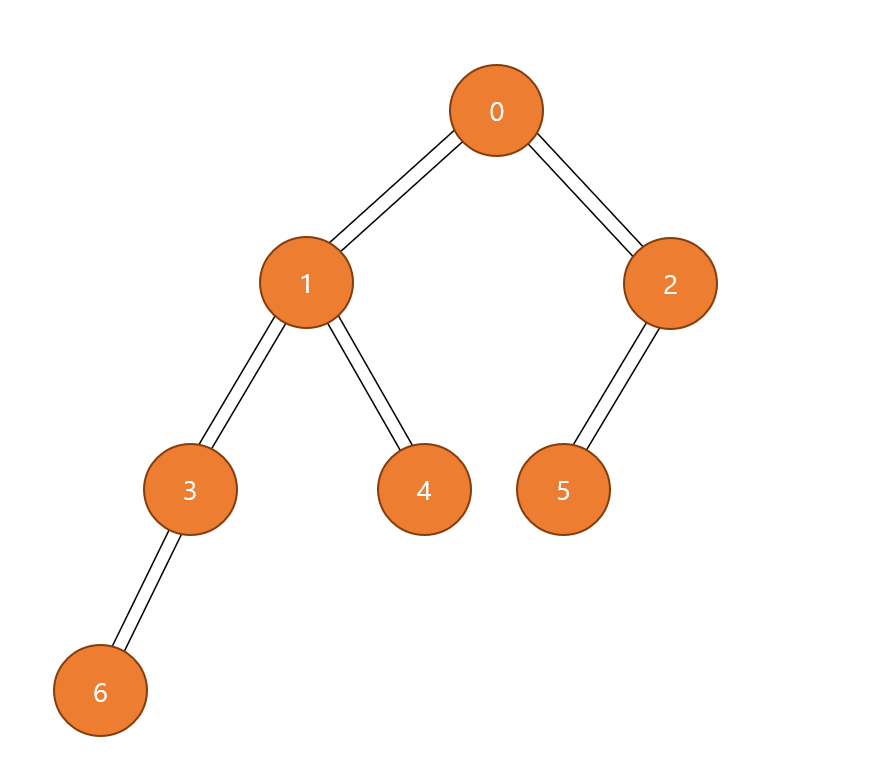
Queue의 front인 6번 pop
------------------------------------------
Queue - []
queue에 추가될 번호가 없고 queue가 비었으므로 탐색 완료
∴방문 순서: 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
Implementation
1. 시작 정점을 Queue에 push
2. Queue의 front node x를 방문 표시(visited[x] = 1), Queue를 pop
3. 정점 x와 인접한 정점 중, 방문하지 않은 정점(visited[nxt] = 0)을 Queue에 push
4. Queue가 비어 있다면 break, 그렇지 않다면 2로 돌아간다.
인접행렬로 구현한 BFS 코드로 시간 복잡도는 $O(V^{2})$이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int adj[101][101]; //인접 행렬, size는 100으로 설정
bool visited[101]; //방문했으면 1, 아니면 0
queue<int> q;
q.push(s);
while(!q.empty()){
int x=q.front();
q.pop();
for(int nxt=1; nxt<=n; nxt++){
if(!visited[nxt] && adj[x][nxt]==1){
q.push(nxt);
}
}
}
|
cs |
다음 코드는 인접리스트로 구현한 BFS로 시간 복잡도는 $O(V+E)$이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
vector<int> adj[101]; //인접리스트
bool visited[101]; //방문했으면 1, 아니면 0
void bfs(int st)
{
queue<int> q;
q.push(st); //시작 정점 삽입
while(!q.empty()){
int x=q.front(); //현재 정점
q.pop();
for(int nxt : adj[x]){ //인접한 정점 탐색
if(!visited[x]){ //방문하지 않았다면
q.push(i); //탐색
}
}
}
}
|
cs |
Flood Fill by BFS
DFS 글에서 소개한 Flood Fill을 BFS를 통해 가능하다. DFS로도 가능하지만 특히 BFS 알고리즘은 미로 탐색에서 활용된다. DFS 알고리즘은 한 분기 씩 나누어 탐색하기 때문에 exit가 아닌 분기로 탐색할 경우, 비효율적으로 탐색을 하게 되는 것에 비해, BFS 알고리즘을 이용하면 연산량이 오직 exit와의 거리에 의해 결정되므로 더욱 효율적으로 동작하기 때문에 BFS 알고리즘을 미로 탐색에 사용한다.
https://www.acmicpc.net/problem/2178
2178번: 미로 탐색
첫째 줄에 두 정수 N, M(2 ≤ N, M ≤ 100)이 주어진다. 다음 N개의 줄에는 M개의 정수로 미로가 주어진다. 각각의 수들은 붙어서 입력으로 주어진다.
www.acmicpc.net
DFS에서의 Implementation과 마찬가지로, 현재 위치에서 위쪽, 아래쪽, 왼쪽, 오른쪽으로 이동 가능한지를 확인하고, 갈 수 있다면 그 위치를 큐에 넣어주어 구현하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n, m;
string v[101];
//x에 더해질 값
int dx[4]={-1, 1, 0, 0};
//y에 더해질 값
int dy[4]={0, 0, -1, 1};
bool visited[101][101];
//위치에 대한 정보
struct info{
int x, y, cost;
};
queue<info> q;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i=0; i<n; i++){
cin >> v[i];
}
q.push({0, 0, 1});
visited[0][0]=1;
while(!q.empty()){
int x=q.front().x;
int y=q.front().y;
int cost=q.front().cost;
//도착했다면
if(x==n-1 && y==m-1){
cout << cost << "\n";
break;
}
q.pop();
for(int i=0; i<4; i++){
int nx=x+dx[i], ny=y+dy[i];
//인접한 칸이 범위 바깥이라면
if(nx<0 || ny<0 || nx>=n || ny>=m){ continue; }
//갈 수 있는 칸이고, 아직 방문하지 않았다면
if(v[nx][ny]=='1' && visited[nx][ny]==0){
visited[nx][ny]=1;
q.push({nx, ny, cost+1});
}
}
}
return 0;
}
|
cs |
'Algorithm' 카테고리의 다른 글
| 그리디 알고리즘(greedy) (0) | 2021.02.11 |
|---|---|
| 분할 정복(Divide and Conquer) (0) | 2021.02.11 |
| [ Graph ] 깊이 우선 탐색 (DFS, Depth-First-Search) (1) | 2021.02.11 |
| 그래프란? (0) | 2021.02.11 |
| [ DP ] 동적 계획법 (Dynamic Programming) (0) | 2021.02.11 |