Depth-First-Search
탐색 공간을 탐색하기 위해 다양한 탐색 방법이 존재한다. Bruteforce, 선형 탐색, Backtracking 등이 그 예시이다. 비선형적인 탐색 공간을 탐색하기 위해서는 재귀 기반 탐색 등이 요구된다. 이는 단순한 순차 탐색으로는 비선형 공간을 탐색하기 어렵다는 것을 의미한다.
비선형 공간 중, 가장 일반적인 형태인 Graph에서의 탐색 방법을 알아보자. 이전의 Backtracking 글에서는 이미 수차례 비선형 탐색 공간에서 재귀 탐색을 시행해왔다. 본 글에서는 그래프 탐색의 종류에 대해 더욱 엄밀하게 이해하고자 한다.
그래프 공간에서의 탐색은 방식(탐색 순서)에 따라 크게 2가지로 나뉜다. DFS, BFS가 그 종류이다. DFS(Depth-First-Search)는 재귀 기반(Stack Based)의 탐색 방법으로, 탐색 공간에서 분기(Branch) 별로 탐색을 한다는 특징을 가진다. 즉, 한 Branch를 끝까지 탐색하고, 올라오다가 다른 분기를 발견하면 또 쭉 내려가 탐색하는 방식을 취한다. BFS에 비해서는 구현이 간단하다는 특징이 있다.

탐색을 $0$번 정점에서 시작할 것이다.
방문한 정점은 색을 주황색으로 표시하고 현재 위치를 화살표로 나타낼 것이며, 탐색의 조건을 만족하기 위해 한 번 방문한 정점은 다시 방문하지 않는다.
$0$번 정점에서 시작해서 $1$번 정점으로 가고

$1$번 정점에서 $3$번 정점으로 가고

$3$번 정점에서 $6$번 정점으로 간다.

$6$번 정점에서 더 이상 갈 곳이 없으므로 바로 전의 $3$번 정점에서 다음으로 갈 곳을 선택한다.


$3$번 정점에서 더 이상 갈 곳이 없으므로 바로 전의 $1$번 정점에서 다음으로 갈 곳을 선택한다.

이처럼 dfs는 $0$->$1$->$3$->$6$처럼 한 분기를 깊게 들어가다가 더 이상 탐색이 불가능하면 Backtracking하여 방문하지 않은 분기를 찾아 탐색한다.
$1$번 정점에서 $4$번 정점으로 이동할 수 있으므로 $4$번 정점으로 이동한다.

$4$번 정점에서 더 이상 방문할 정점이 없으므로 바로 전의 $1$번으로 돌아간다.
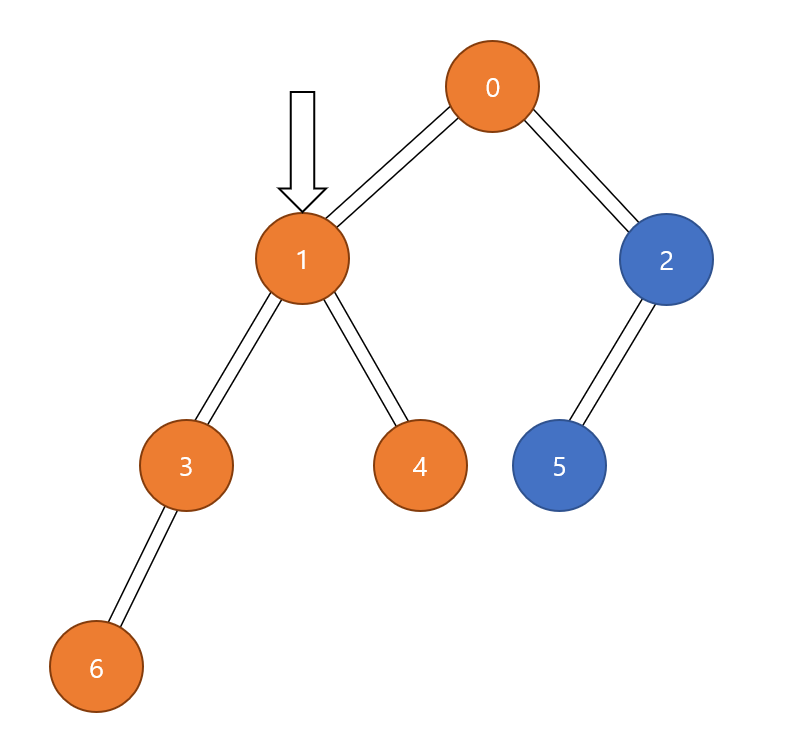
$1$번 정점에서 더 이상 방문할 정점이 없으므로 바로 전의 $0$번으로 돌아가서 $2$번 정점으로 향한다.

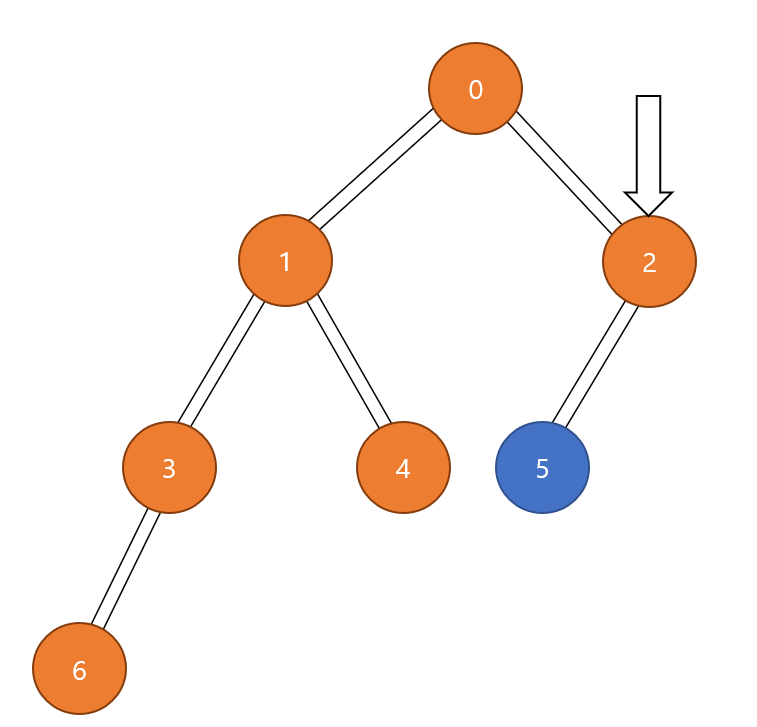
$2$번 정점에서 $5$번 정점으로 가고 이제 방문할 정점이 없으므로 탐색을 종료한다.

∴ $0$ -> $1$ -> $3$ -> $6$ -> $4$ -> $2$ -> $5$
Implementation
구현 방법에는 2가지 방법이 있는데, 순환 호출을 이용한 방법과 Stack을 사용하는 방법이 있다.
1. 재귀 기반(순환 호출) 구현 : 기존에 하던 Backtracking과 거의 유사하다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
int adj[101][101];
bool visited[101];
void dfs(int x)
{
//이미 방문하였으면 종료
if(visited[x]) return;
visited[x]=1; //방문 표시
for(int nxt=1; nxt<=n; nxt++){ //인접한 노드들 탐색
if(visited[nxt]==0 && adj[x][nxt]){ //연결되어 있고 방문하지 않은 노드라면
dfs(nxt); //탐색
}
}
}
|
cs |
$adj$는 인접행렬이고 $visited$는 방문 여부를 확인하는 Array이다. 반복문을 통해 모든 정점을 확인하여 인접 여부, 방문 여부를 확인하여 재귀 호출을 시행한다. $V$개의 정점을 탐색하기 위해 인접한 노드를 탐색하는데 $V$번 연산을 했으므로 시간복잡도는 $O($$V^{2}$$)$이다.
아래 코드는 인접 리스트를 이용한 구현이다. 이 때 $V$개의 정점을 탐색하기 위해 연산이 간선의 개수인 $E$번 만큼 실행되므로 시간복잡도는 $O(V + E)$이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
vector<int> adj[101]; //vector를 이용한 인접리스트
bool visited[101];
void dfs(int x)
{
if(visited[x]) return;
visited[x]=1; //방문 표시
for(int nxt : adj[x]){ //인접한 정점들 탐색
if(visited[x]==0){ //방문하지 않았으면
dfs(nxt); //탐색
}
}
}
|
cs |
2. Stack 기반의 구현
재귀 호출의 구조가 스택 메모리의 구조와 동일하므로 Stack으로 구현하는 것 또한 가능하다. 재귀 호출하는 자리에 Stack.push를 시행해주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
vector<int> adj[101]; //vector를 이용한 인접리스트
bool visited[101];
void dfs(int x)
{
stack<int> st;
st.push(x);
while(!st.empty){
int a=st.top(); //stack의 top에 있는 정점
st.pop();
for(int nxt : adj[x]){ //인접한 정점 탐색
if(!visited[nxt]){ //방문하지 않았으면
st.push(nxt); //탐색
}
}
}
}
|
cs |
Flood Fill
DFS 알고리즘을 통해 그래프를 순회하는 방법을 배웠는데 이제 2차원 배열을 그래프로 나타내고 순회하는 방법을 배워볼 것이다. 이는 2차원 맵의 모든 칸을 탐색하며 채우는 방법으로, 탐색을 통해 공간을 채운다고 해서 Flood Fill이라는 방법으로도 불린다.
https://www.acmicpc.net/problem/2667
2667번: 단지번호붙이기
<그림 1>과 같이 정사각형 모양의 지도가 있다. 1은 집이 있는 곳을, 0은 집이 없는 곳을 나타낸다. 철수는 이 지도를 가지고 연결된 집의 모임인 단지를 정의하고, 단지에 번호를 붙이려 한다. 여
www.acmicpc.net
이 문제에서는 2차원 배열에서 1로 되어 있는 부분과 0으로 되어 있는 부분이 존재하고, 1로 되어 있는 인접한 칸들은 같은 단지라고 할 때, 단지의 개수를 구하는 문제이다.
DFS를 통해 1로 연속되어 채워져 있는 공간을 탐색할 것이다. 따라서 DFS 재귀 함수의 인자로는 현재의 위치 좌표를 표현하는 x, y가 필요할 것이다. 이 때, 인접한 칸인 (x+1, y), (x, y+1), (x-1, y), (x, y-1)에 대해 갈 수 있는지( 그 칸의 값이 1인지, 인접한 칸이 맵 밖으로 나가지는 않는지 )를 확인한 후, 해당 방향으로 재귀 호출을 해준다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
char s[MAX_N][MAX_N];
bool visited[MAX_N][MAX_N];
int dx[4]={-1, 1, 0, 0};
int dy[4]={0, 0, -1, 1};
int cnt=0;
void dfs(int x, int y)
{
// 해당 칸에 방문했음을 표시
visited[x][y] = 1;
// 칸을 방문할 때마다 cnt를 증가시켜 방문하는 칸을 Counting
cnt++;
//위, 아래, 왼쪽, 오른쪽 칸을 차례대로 탐색
for(int i=0; i<4; i++){
// (x, y)에 (dx[i], dy[i])를 각각 더해보면 (nx, ny)가 이웃칸이 됨을 확인할 수 있다
int nx=dx[i]+x, ny=dy[i]+y;
//인접한 칸이 맵을 벗어나거나 그 칸의 값이 0이라면 이동할 수 없다
if(nx<0 || ny<0 || nx>=n || ny>=n || s[nx][ny]=='0') continue;
//이동이 가능하다면 인접한 칸으로 이동한다
dfs(nx, ny);
}
}
|
cs |
2중 반복문을 통해 2차원 배열의 각 칸에 대해 아직 방문하지 않은 칸이라면 dfs를 해준다. dfs는 현재 칸에서 인접해 있는 1로 된 모든 칸을 방문하는 역할을 한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n;
string v[26];
//x에 더해질 값
int dx[4]={-1, 1, 0, 0};
//y에 더해질 값
int dy[4]={0, 0, -1, 1};
int cnt=0;
vector<int> ans;
void dfs(int x, int y)
{
//해당 칸에 방문했음을 표시
v[x][y]='0';
//방문하는 칸의 개수를 센다
cnt++;
//위, 아래, 왼쪽, 오른쪽 칸을 차례대로 탐색
for(int i=0; i<4; i++){
int nx=dx[i]+x, ny=dy[i]+y;
//인접한 칸이 배열을 벗어나거나 그 칸의 값이 0이라면
if(nx<0 || ny<0 || nx>=n || ny>=n || v[nx][ny]=='0'){ continue; }
//이동이 가능하다면 인접한 칸으로 이동한다.
dfs(nx, ny);
}
}
int main()
{
scanf("%d", &n);
for(int i=0; i<n; i++){
cin >> v[i];
}
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(v[i][j]=='1'){
dfs(i, j);
ans.push_back(cnt);
cnt=0;
}
}
}
cout << ans.size() << "\n";
sort(ans.begin(), ans.end());
for(int i : ans){
cout << i << "\n";
}
return 0;
}
|
cs |
'Algorithm' 카테고리의 다른 글
| 분할 정복(Divide and Conquer) (0) | 2021.02.11 |
|---|---|
| [ Graph ] 너비 우선 탐색 (BFS, Breadth-First-Search) (1) | 2021.02.11 |
| 그래프란? (0) | 2021.02.11 |
| [ DP ] 동적 계획법 (Dynamic Programming) (0) | 2021.02.11 |
| [ Sort ] 다양한 정렬 방법 (0) | 2021.02.11 |