- 최단 경로 알고리즘
가중치 그래프에서 정점 간의 최단 경로를 구해야 하는 문제들은 많이 있다. 최단 경로란, 정점 $u$에서 $v$까지 가는데 거치는 간선의 가중치들의 총합을 말한다. 일상생활에서 최단 경로 알고리즘이 사용되는 예시로는 내비게이션(길찾기) 알고리즘이 있다.
최단 경로를 구하는 문제는 어떤 정점 $v$에서 다른 정점 $u$까지 가는 최단 경로를 구하거나, 어떤 정점 $u$에서 다른 모든 정점들까지 가는 최단 경로를 구하는 등 다양하게 사용된다.
다익스트라나 플로이드 알고리즘을 이용해 최단 경로를 구할 때에는 간선의 가중치가 모두 양수여야한다. 그 이유는 음수 간선에 의해 최단 경로가 계속 갱신되어 무한 루프에 빠질 수 있기 때문이다. 이에 대해서는 벨만포드 알고리즘의 글에서 자세하게 다룰 것이니 이 정도만 알고 넘어가도 무방하다. 일반적인 그래프에선 가중치가 양수지만 가중치가 음수인 그래프도 존재하기 때문에 이 때는 다른 방법을 이용한다.
가중치가 음수일 때는 벨만 포드 알고리즘을 이용하는데 이는 다익스트라, 플로이드 알고리즘을 공부하고 하면 된다.
- Dijkstra 알고리즘
어떤 정점에서 다른 정점의 최단 경로를 저장하는 dist 배열을 만들어 주고 dist 배열을 무한(매우 큰 수)으로 초기화해준다.(단 시작점은 0으로 초기화한다)
그리고 시작점부터 시작해서 인접한 정점으로 이동해주면서 최단 경로를 갱신해주는데, 핵심은 다음으로 이동한 정점의 최단경로(dist[next])가 현재 정점에서의 비용(dist[cur])과 간선의 가중치(cost)의 합보다 크다면 dist[next] 값을 갱신해주는 아이디어이다.
다음과 같은 그래프를 예로 들어보자.
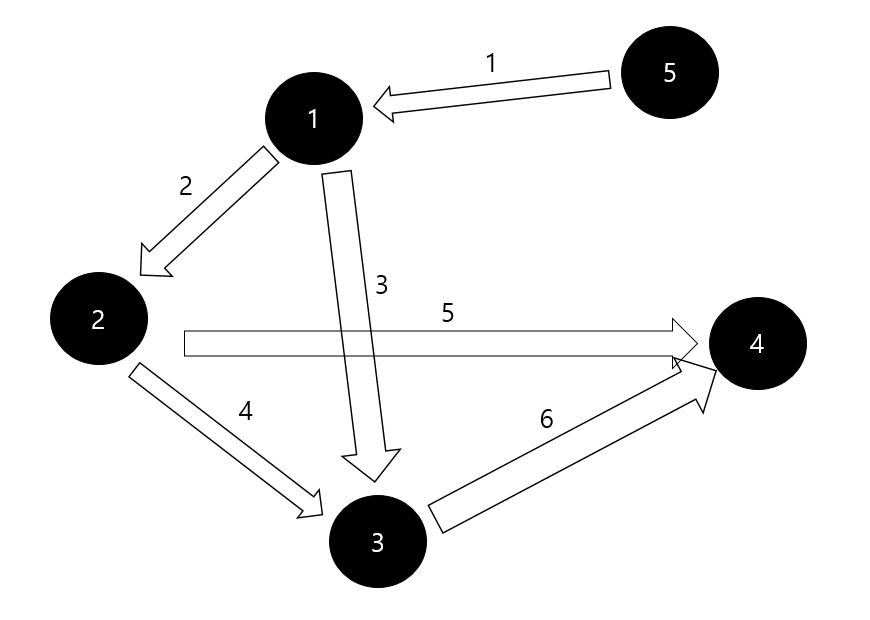
먼저 시작 정점으로부터의 최단 경로의 비용을 저장하는 $dist$배열을 만들고 이 배열을 ∞로 초기화할 것이다.(아직 거리를 구하지 않았기 때문이다, 단 시작 정점인 1번 정점은 0으로 초기화 해주어야 한다.)

이제 $1$번 정점부터 다른 정점들로 가는 최단 경로를 구할 것인데 BFS와 비슷한 방식으로 작동하지만 queue가 아닌 priority queue를 사용할 것이다. 그 이유는 현재 queue안에 있는 정보들을 거리가 작은 순으로 정렬하면서 탐색할 것이기 때문이다.
priority queue에는 (현재 정점, 지금까지 이동한 거리)가 저장되어 있다.
먼저 시작 정점인 $1$번 정점을 넣는다.
- 정점: 1 이동한 거리: 0
그 다음 $1$번 정점에서 갈 수 있는 정점의 최단 경로를 갱신한다. $2$, $3$번 정점은 현재 최단경로가 ∞이므로 갱신된다.

priority queue에 2, 3번 정점을 넣는다.
- 정점: 2 이동한 거리: 2
- 정점: 2 이동한 거리: 3
그 다음 priority queue의 top인 2번 정점과 인접한 정점들을 확인한다.
2번 정점에서 3번 정점으로 갈 수 있지만 (현재 이동거리)+(3번 정점으로 이동할 거리) = 6이고 이는 현재 dist[3]보다 크므로 갱신되지 않고 priority queue에 추가되지도 않는다.
2번 정점에서 4번 정점으로 갈 수 있고 dist[4]가 (현재 이동거리)+(4번 정점으로 이동할 거리)=7보다 크므로 갱신해준다.

- 정점: 3 이동한 거리: 3
- 정점: 4 이동한 거리: 7
3번 정점에선 6번 정점으로 갈 수 있지만 dist[6]이 (현재 이동거리)+(6번 정점으로 이동할 거리)=9보다 작으므로 갱신하지 않는다.
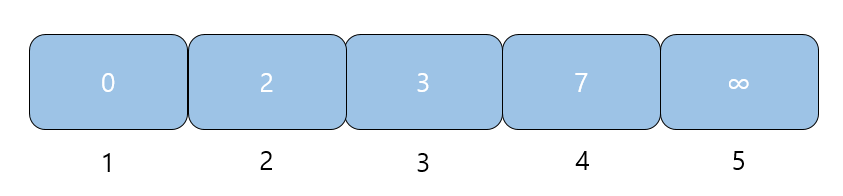
- 정점: 4 이동한 거리: 7
4번 정점에선 갈 수 있는 정점이 없으므로 pop하고 priority queue가 비므로 종료한다.
- 다익스트라 알고리즘의 정당성 증명
그렇다면 위 방식으로 최단 경로를 구할 수 있음을 증명할 것이다. 만약 다익스트라 알고리즘을 배우고 활용하는 것이 주 목적이라면 바로 아래의 '구현'을 읽으면 된다.
다익스트라 알고리즘에서 현재의 정점을 v라고 하고, v와 인접한 정점에 대해 우선순위 큐에 넣어주는 작업을 마무리했다면(v에 대한 방문이 종료되었다면), dist[v]는 최단 경로 값이고, 더 이상 갱신되지 않는다. 이것이 왜 성립하는지를 증명하자.
먼저, 이미 방문한 정점 집합을 S = {v1, v2, ..., vk}라고 하자. 위 문장에 따르면 u에 대한 방문을 끝내면 dist[u]가 시작점에서 u까지의 최단경로 값이다. 이를 증명해보자.
dist[u]의 값은 방문된 정점들의 최단 경로인 dist[v1], ..., dist[vk]들로부터 계산되었을 것이고, 거리값은 항상 양수이므로 dist[u] = dist[V] + cost(V ∈S), dist[u] > dist[v1], dist[v2], ..., dist[vk]임이 보장된다.(A)
그런데, 만약 dist[u]가 S에 속해있지 않은 정점의 dist 값으로부터 계산된다면 어떻게 될까? 그렇다면 dist[u]가 갱신될 수도 있지 않을까? 아직 방문하지 않은 정점 t에 대해, dist[t]가 추후에 갱신되어 dist[t] < dist[u]가 된다고 하자. 그렇다면 dist[t] + cost < dist[u]가 되어 dist[u]가 갱신될 수도 있다. 하지만 위에서 A에 의해 dist[t]는 이전에 방문된 모든 정점들의 dist 값보다 커야 한다. 따라서 이는 모순이므로 dist[u]는 t에 의해 갱신될 수 없다. 즉, dist[u]는 최단경로값이다.
구현
초기화
먼저 dist 배열을 ∞(이 문제에서 나올 수 없는 큰 수)로 초기화하고 시작점은 0으로 설정한다.(자기 자신으로의 최단 경로는 0이기 때문이다.)
|
1
2
|
for(int i=1; i<=n; i++) dist[i]=0x7fffffff;
dist[s]=0;
|
cs |
정점 클래스
priority queue에 넣을 정보(현재 정점, 이동 거리)를 저장하는 구조체를 만든다.
|
1
2
3
4
5
6
7
8
9
10
11
|
struct Node{
int node;
long long cost;
};
vector<Node> adj[1001];
bool operator < (Node a, Node b)
{
return a.cost>b.cost;
}
|
cs |
다익스트라 알고리즘 코드
다음에 탐색할 정점의 최단 경로가 현재까지 이동거리+다음정점으로 갈 거리보다 크다면 값을 갱신해준다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
priority_queue<Node> q;
q.push({s, 0});
while(!q.empty()){
int x=q.top().node;
q.pop();
for(Node i : adj[x]){
int nxt=i.node; //다음에 탐색할 정점
long long nxtCost=dist[x]+i.cost; //현재까지의 이동거리 + 다음 정점으로 갈 거리
if(dist[nxt]>nxtCost){
dist[nxt]=nxtCost;
q.push({nxt, dist[nxt]});
}
}
}
|
cs |
전체 코드
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K≤V)가 주어진다.
www.acmicpc.net
http://boj.kr/2179821a9a8346d99f794201bf86f0f7
공유 소스 보기
www.acmicpc.net
플로이드 알고리즘
플로이드 알고리즘은 모든 정점 쌍 간의 최단 경로를 구하는 알고리즘으로, 최단경로를 계속 갱신하면서 해를 구하는 방식이 dijkstra 알고리즘과 유사하다.
즉, 어떤 정점 i에서 j로 가는것보다 정점 i에서 정점 k를 거쳐서 정점 j로 가는 것이 더 빠르다면 갱신해주는 방식으로 이루어진다. 정점 i, j, k는 반복문을 이용해 지정해주어야 할 것이다.
|
1
2
3
4
5
6
7
8
9
10
|
for(int k=1; k<=n; k++){
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
//i->j 보다 i->k->j가 더 빠르다면
if(dist[i][j]>dist[i][k]+dist[k][j]){
dist[i][j]=dist[i][k]+dist[k][j];
}
}
}
}
|
cs |
코드는 매우 짧지만 시간 복잡도는 $O(N^{3})$으로 비효율적이다. 보통 문제에서 $N$의 범위가 약 100 정도까지이면 사용할 수 있다.
전체 코드
https://www.acmicpc.net/problem/11404
11404번: 플로이드
첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가
www.acmicpc.net
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int n, m;
int dist[101][101];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(i!=j){ dist[i][j]=999999999; }
}
}
while(m--){
int u, v, w;
cin >> u >> v >> w;
dist[u][v]=min(dist[u][v], w);
}
for(int k=1; k<=n; k++){
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(dist[i][j]>dist[i][k]+dist[k][j]){
dist[i][j]=dist[i][k]+dist[k][j];
}
}
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(dist[i][j]==999999999){ cout << 0 << " "; }
else{ cout << dist[i][j] << " "; }
}
cout << "\n";
}
return 0;
}'Algorithm' 카테고리의 다른 글
| [ DP ] 비트마스크 (BitMask), BitDp (0) | 2021.07.31 |
|---|---|
| 컨벡스 헐(Convex Hull) 알고리즘 (0) | 2021.03.27 |
| [ Graph ] 단절점, 단절선 (Articulation Point, Bridge) (1) | 2021.03.13 |
| [ Query ] Sqrt Decomposition (제곱근 분할법) (2) | 2021.02.25 |
| [ Query ] 오일러 경로 테크닉 (Euler Tour Technique) (2) | 2021.02.18 |