Binary Search
데이터를 효율적으로 탐색하기 위해서는 탐색 공간이 효율적으로 구성되었는지와, 탐색 알고리즘이 잘 설계되어 있는지를 고려해야 한다. 탐색 알고리즘이 잘 설계되었다는 것은 해가 될 가능성이 높은 데이터를 위주로 탐색한다는 것으로, 해를 찾기 위한 연산 횟수의 상한(upper bound)이 작을수록 좋다. 이분탐색은 그러한 탐색 횟수의 상한을 $ log N $으로 보장하는 탐색 알고리즘이다. Binary Search는 매 시행마다 탐색 구간을 절반씩 줄여나가면서 탐색을 진행하는 알고리즘이다. 일반적인 탐색 방법과 비교하기 위해 다음과 같은 문제를 해결해보자.
수열에서 정수 $K$는 어느 인덱스 값을 가지는가?( $K$ ∈ $[1, N]$ )
이를 Bruteforce 기법을 통해 해결하면 탐색 공간인 $[1, N]$의 $N$개의 원소를 모두 확인하는 $O(N)$의 알고리즘을 설계할 수 있다. 하지만 원소를 찾는 연산을 여러 번 반복하는 쿼리(Query, 질의) 형태의 입력이 주어진다면, 이를 단순하게 일일이 확인하는 것은 너무 비효율적인 작업일 것이다. 우리는 언젠가 수학 잡지 등에서 이러한 해법을 본 적이 있을 것이다.
$[N/2]$와 $K$를 비교한다, $K$가 $[N/2]$보다 크다면 $[[N/2], N]$을 탐색하고 아니라면 $[1, [N/2]]$를 탐색한다...
즉, 구간의 중앙값을 확인하고, 중앙값과 탐색값의 대소비교를 통해 탐색에 필요없는 구간을 배제하며 탐색하는 방법이다. 하지만 이러한 방법은 일반적으로는 성립하지 않지만 이 문제에 대해서는 예외적으로 성립한다. 왜냐하면 이 문제는 탐색 공간이 정렬되어 있기 때문이다. 탐색 공간이 정렬되어 있기 때문에, 중앙값과 탐색값을 비교한다면 분할된 두 구간 중 어느 한 구간에 대해서는 그 구간에 절대 해가 존재할 수 없음을 보장할 수 있게 되기 때문이다.
즉, 1부터 1,000까지의 수 중 50의 index를 찾는다고 하면, 중앙값인 500과 50을 비교함으로써 [500, 1,000]의 구간은 절대 해가 될 수 없음을 보장할 수 있다. 왜냐하면 탐색 공간이 정렬되어 있기 때문에 [500, 1,000] 내의 모든 원소가 50보다 크다는 것은, 500과 50을 비교하는 것만으로도 충분하게 알 수 있기 때문이다.
Binary Search는 위와 같은 과정을 반복하며 탐색 구간을 계속 절반 씩 줄여나가는 탐색 방법이다. 이를 정리하면 다음과 같다.
- 탐색 구간의 중앙값 $m$과 내가 찾고자 하는 값인 $target$을 비교한다.
- $target<m$이라면 𝑡𝑎𝑟𝑔𝑒𝑡이 $[1, m-1]$에 존재하므로 탐색 범위를 $[1, m-1]$로 바꾸고 위 과정으로 돌아간다.
- $target>m$이라면 𝑡𝑎𝑟𝑔𝑒𝑡이 $[m+1, n]$에 존재하므로 탐색 범위를 $[m+1, N]$으로 바꾸고 위 과정으로 돌아간다.
- $target == m$이라면 값을 찾았으므로 종료한다.
How to Work

위 상황은 탐색 공간인 수열 {1,2,3,4,5,6,7,8,9,10}에서 7을 찾고자 하는 상황이다. 이 때, 단순히 탐색 범위 내의 모든 원소를 일일이 확인하는, 즉 1번째부터 10번째까지 원소들을 모두 확인한다면 $O(N)$으로 해를 구할 수 있다. 하지만 이분탐색은 $O(logN)$의 시간복잡도를 보장하게 되므로, 만약 데이터가 10억 개 정도일 때 Bruteforce 기법은 최악의 경우에 10억 번 계산하게 되지만 Binary Search로는 30 여 번 만에 계산이 끝나게 된다.
초기 탐색 범위의 중앙값은 5
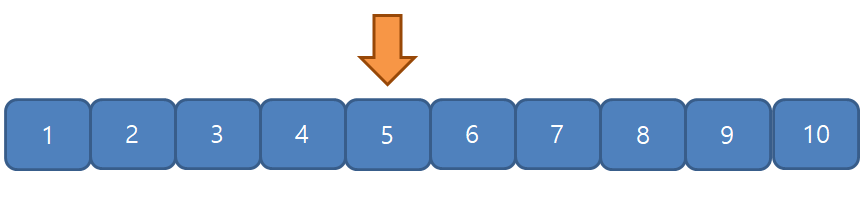
$target$은 5보다 크므로 탐색 구간이 [6, 10]이다. [6, 10]8이고,

$target$은 8보다 작으므로 탐색 구간이 [6, 7]이다. [6, 7]의 중앙값은 6이고,

$target$은 6보다 크므로 탐색 구간은 [7, 7]이다.

구간의 중앙값과 $target$이 같으므로 구하고자 하는 7을 찾았다.
$target$과 특정 구간의 상한 혹은 하한과 비교함으로써 그 구간을 배제할 수 있다는 것은 데이터의 정렬성을 통해 보장된다. 이를 위해 Binary Search를 이용할 수 있도록 데이터의 순서를 조정하는 것이 중요하다.
Implementation
탐색 범위를 설정하기 위한 변수 s, e가 필요하여, 구간 [s, e]를 줄여나가면서 탐색을 진행한다.
현재 탐색하고 있는 구간 [s, e]의 중앙값인 mid = (s+e)/2를 target과 비교하여 구간을 줄이는 과정을 반복한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include <iostream>
using namespace std;
int N;
int arr[1001];
int main()
{
//입력으로 주어지는 정수는 오름차순이라고 가정
scanf("%d", &N);
for(int i=1; i<=N; i++){
scanf("%d", &arr[i]);
}
//찾고자 하는 값 K
scanf("%d", &K);
int s = 1, e = N;
while(s<=e){
int mid=(s+e)/2;
//s와 e의 중간
if(arr[mid]==K){
printf("Found!\n");
break;
}
else if(arr[mid]>K) e=mid-1;
else s=mid+1;
}
return 0;
}
|
cs |
Parametric Search
Parametric Search는 한국어로 하면 '매개 변수 탐색'이다. 매개 변수라는 것은 기존에 존재하는 변수 간의 표현 관계를 다르게 하기 위해 사용하는 임의로 설정한 변수이다. 탐색을 진행하기 위해서는 탐색 공간을 나타내기 위한 인자(parameter)가 필수적이다. 예를 들어 주사위를 굴려 나올 수 있는 경우를 탐색할 때는 인자 x가 주사위의 눈 수를 나타내는 것이다. 이러한 인자가 명확하게 주어지지 않은 경우에 해를 구해야 하는 경우가 존재할 수 있다. 다르게 말하자면 탐색의 기준으로 잡을 수 있는 인자를 임의로 설정해서 탐색을 효율적으로 하고자 하는 아이디어가 Parametric Search이다.
그렇다면 내용이 크게 2가지로 나뉜다. 첫 번째로 인자는 어떻게 잡을 것인가? ( 잡을 수 있는 인자라는 것이 무엇인가? )이고 두 번째로는 탐색을 어떻게 효율적으로 한다는 것인가에 대한 내용이다. 두 번째에 대해 먼저 답을 하자면, Binary Search를 통해 탐색의 효율성을 보장할 것이다. 즉, 일반적인 문제를 Binary Search가 적용 가능한 문제로 바꾼다는 아이디어가 Parametric Search의 정의이다. 인자를 어떻게 잡는가는 예시 문제를 통해 설명할 것이다.
BOJ 2110 공유기 설치 : 문제를 요약하자면, 수직선 위에 N개의 집이 있고, 집 중 일부(C개)를 골라 공유기를 설치한다. 이 때 공유기 간 간격의 최솟값을 최대화시키고자 하는 것이다. 이렇게 최솟값을 최대화, 최댓값을 최소화라는 문구는 Parametric Search를 암시하는 경우가 많다.
이 문제를 살짝 변형하여, 답을 고정시킨 상태에서 그 값이 답이 될 수 있는지 확인해보는 것이 더욱 효율적일 수 있다.
즉, 공유기 간 간격의 최솟값을 X라고 했을 때, 공유기 간 간격이 X 이상이 되도록 집을 고를 수 있는가?에 대한 참/거짓 여부를 판별하는 것을 간단하게 구현할 수 있다는 것이다.
이는 해를 구하는 문제를 'f(x)가 참이 될 수 있는가?'를 만족하는 최소/최대의 x를 구하는 문제로 바꾸었다. 이렇게 임의의 x에 대해 f(x)의 참/거짓 여부를 판단하는 문제를 결정문제라고 한다.
그러면 집을 간격이 X 이상이 되도록 고르는 문제는 간단하게 아래와 같이 구현 가능하므로, X를 0부터 일일이 탐색해보며 , f(X)가 참이 되도록 하는 최대의 X 값을 구하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
typedef long long ll;
const int MAX_N = 200005;
const int INF = 1e9;
int N, C;
ll x[MAX_N];
bool f(int X)
{
// last : 마지막에 고른 집의 x좌표
// cnt : 고른 집의 개수
int last = -INF, cnt = 0;
for(int i=0; i<N; i++){
//마지막에 고른 집과 현재 고르려는 집의 간격이 X 이상이면
if(x[i]-last>=X){
cnt++, last = x[i];
}
}
return cnt>=C;
}
|
cs |
이렇게 집을 C개 고르는 것이 가능한지 판별하는 함수 f를 $O(N)$에 구현했다. 그러면 X 값을 일일이 확인하며 최대의 X 값을 구해야 하는데 그러면 시간복잡도가 $O(N^2)$이 되므로 더욱 효율적인 방법이 필요하다.
X 값에 따른 f의 T/F 여부를 관찰하면 얻을 수 있는 사실은 X가 0부터 증가함에 따라 f의 T/F 여부가 T, T, T, ...로 진행되다가 어느 순간부터 T, T, F, F, F, ...가 된다는 것을 알 수 있다. 즉, X의 증가에 따른 T/F 여부가 이분적으로 나타나므로 이분 탐색을 통해 마지막으로 T가 되는 X 값을 구해준다면 답을 찾을 수 있다.

결론을 정리하자면, Parametric Search는 탐색을 진행할 인자를 임의로 결정(기존의 인자는 x좌표였지만, 인자를 공유기 간 최소 간격이라는 매개 변수로 설정)하여 탐색 문제를 결정 문제로 변형하는 알고리즘이고, 결정 문제의 답이 매개 변수에 증가에 따라 이분적(T, T, ..., T, F, F, ....)로 나타나므로 이분 탐색을 이용하여 T가 되는 최대의 매개변수 값 or F가 되는 최소의 매개변수 값을 구하는 방법이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAX_N = 200005;
const int INF = 1e9;
int N, C;
ll x[MAX_N];
bool f(int d)
{
int last = -INF, cnt = 0;
for(int i=0; i<N; i++){
if(x[i]-last>=d){
cnt++, last = x[i];
}
}
return cnt>=C;
}
int main()
{
scanf("%d %d", &N, &C);
for(int i=0; i<N; i++) scanf("%lld", &x[i]);
sort(x, x+N);
int s = -1, e = 1000000005;
while(s+1<e){
int mid = s + e >> 1;
if(f(mid)) s = mid;
else e = mid;
}
printf("%d\n", s);
return 0;
}
|
cs |
'Algorithm' 카테고리의 다른 글
| 그래프란? (0) | 2021.02.11 |
|---|---|
| [ DP ] 동적 계획법 (Dynamic Programming) (0) | 2021.02.11 |
| [ Sort ] 다양한 정렬 방법 (0) | 2021.02.11 |
| [ Search ] 백트래킹 (BackTracking) (0) | 2021.02.11 |
| [ Search ] 완전 탐색 (BruteForce Algorithm) (0) | 2021.02.11 |