Union Find

Union Find란?

 

Union Find는 상호 배타적 집합을 표현하는 자료구조이다.

 

전체 집합을 교집합이 없는 부분집합들로 나누어서 저장한다.

 

상호 배타적: 부분 집합 간의 교집합이 없다.(공통된 원소가 없다), 모든 부분집합의 합집합은 전체 집합이다.

 

집합을 표현해서 구성 요소 간의 연결 여부 또는 연결성을 가지고 있는지 여부를 따지는 문제에서 많이 사용된다.

 

 

Union Find의 연산

 

1. $find$: 해당 원소가 어느 집합에 속해 있는지 찾기

 

3. $union$: 두 집합을 한 집합으로 합친다.

 

 

Union Find의 구현

 

유니온 파인드는 트리 형태의 자료 구조이므로 각 집합을 하나의 트리 모양으로 표현할 것이다. 

 

 

 

이와 같은 모양의 집합을 트리로 표현하면

 

 

다음과 같이 된다. 이 때 트리의 모양은 표현 방법에 따라 다르게 표현될 수 있다.

 

 

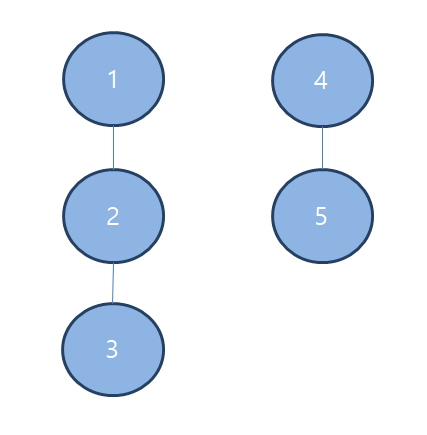
이 그림 또한 같은 집합이다.

 

이를 구현하기 위해 트리를 만드는데 인접리스트가 아닌 일차원 배열로 구현할 것이다.

 

$parent[i]=i$번 노드의 부모 노드

 

 

1) 초기화

 

void init()
{
    for(int i=1; i<=n; i++){ parent[i]=i; }
}

 

자신의 루트 노드를 자신으로 설정한다. 이 때 $parent[i]$를 그냥 $-1$로 초기화해도 된다.

 

2) Find

 

int find(int x)
{
    if(x==parent[x]){ return x; } //루트까지 올라왔으면 집합 번호 반환
    return find(parent[x]);
}

 

재귀함수를 통해 루트 노드까지 올라가는 방식이다.

$6$번 노드에서 루트를 찾아보면

6번의 부모: 3번

3번의 부모: 2번

2번의 부모: 1번

1번에서 1 return

따라서 $6$번 노드의 루트는 $1$번 노드이다.

 

 

이 방식은 실행 시간이 트리의 깊이에 비례하므로 메모이제이션과 비슷한 방식을 사용해볼 것이다.

 

예를 들어 $6$번이 $1$번 집합에 속해 있다는 것을 $find(6)$을 통해 찾았을 때 다시 $find(6)$을 계산해야하는 상황이 올 수도 있다. 그러면 다시 계산해야 하므로 dp에서 했던 메모이제이션 기법과 비슷하게 바꿔볼 것이다.

 

 

int find(int x)
{
    if(x==parent[x]){ return x; } //루트까지 올라왔으면 집합 번호 반환
    return parent[x]=find(parent[x]);
}

 

이 코드대로 해보면 6번의 부모, 3번의 부모, 2번의 부모 모두 1번으로 바뀌게 된다.

 

따라서 트리가 다음과 같은 모양으로 깊이가 대폭 줄어든다.

 

 

이러한 최적화를 경로 압축 최적화라고 한다.

 

노드 $x$에서 루트 노드까지의 경로 상에 있는 모든 노드들이 경로 압축 최적화가 된다.

 

이 때의 시간 복잡도는 상수 시간으로 나온다.

 

3) Union

 

void merge(int x, int y)
{
    x=find(x), y=find(y);
    if(x==y){ return; } //만약 두 원소가 같은 집합에 있다면
    parent[x]=y;
}

 

먼저 두 노드의 루트 노드를 각각 구해주고 만약 루트 노드가 같으면 같은 집합에 속해 있는 것이므로 종료해준다.

 

만약 두 노드가 다른 집합이라면 루트 노드끼리 간선을 만들어준다.

 

 

 

전체 코드

 

https://www.acmicpc.net/problem/1717

1717번: 집합의 표현

 

#include <iostream>

using namespace std;

int u[1000001];

int find(int x)
{
    return x==u[x] ? x : u[x]=find(u[x]);
}

bool merge(int x, int y)
{
    x=find(x); y=find(y);
    if(x==y){ return 0; }
    u[y]=x; return 1;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    int n, m; cin >> n >> m;
    for(int i=1; i<=n; i++){ u[i]=i; }
    for(int i=1; i<=m; i++){
        int a, b, c;
        cin >> a >> b >> c;
        if(a==0){
            merge(b, c);
        }
        else{
            if(find(b)==find(c)){ cout << "YES\n"; }
            else{ cout << "NO\n"; }
        }
    }
    return 0;
}