회귀와 분류
머신러닝의 분류 체계는 지도학습(supervised learning), 비지도학습(unsupervised learning), 강화학습(reinforcement learning)으로 구분된다. 특히 지도학습은 정답(레이블, target variable)이 존재하는 데이터에서의 머신러닝이다.
지도학습은 회귀(regression)와 분류(classification)으로 구분되는데, 회귀는 label이 numerical value(정량적인 숫자)이고 분류는 label이 categorical value(비정형적인 클래스)이다.
| 지도학습 | 설명 | 예시 |
| 회귀(Regression) | 예측하고자 하는 값이 실수인 경우 | 공부 시간에 따른 수학 시험 성적(실수) 예측 |
| 분류(Classification) | 예측하고자 하는 값이 범주형(문자)인 경우 | 제품 품질 데이터에 따른 불량품 여부(T or F) 예측 |
예를 들어 공부 시간에 따른 성적 예측은 회귀(regression, 성적이라는 숫자를 예측하는 것)이고, 혈당 수치에 따른 당뇨 여부를 예측하는 것은 분류(classification, 당뇨에 대한 양성/음성 여부를 예측하는 것, 양성/음성은 숫자처럼 연속적일 수 없다)이다.
- 백신 보급 수에 따른 평균 감염률(%) 예측 -> Regression(감염률은 수치적인 값이다)
- 고객의 구매 내역에 따른 등급 분류(프리미엄, 노멀 등) -> Classification(등급의 종류가 정해져 있다)
Linear Regression
앞으로 본 글에서 다룰 데이터는 다음의 조건을 만족한다.
- 데이터는 N개의 데이터 포인트로 구성되어 있다.
- 각 데이터 포인트는 M개의 독립변수(특성)와 종속 변수 1개로 구성되어 있다.
- N은 충분히 커 경향성을 파악하기 적합하다.
선형 회귀(Linear Regression)은 독립 변수와 종속 변수 간 관계가 선형적이라는 가정 하에, 독립 변수와 종속 변수의 선형 관계식(일차함수)을 찾는 알고리즘을 말한다.
쉽게 설명해서 공부 시간 X에 따른 성적 Y를 예측한다면, 선형 회귀는 아래의 조건을 만족하는 두 파라미터 $w_{1}, w_{2}$를 예측하는 것을 목표로 한다.
공부시간 $X$와 성적 $Y$는 $Y = w_{1} X + w_{2}$의 관계를 따를 것이다.

즉, 학습 시간과 시험 성적 간의 분포를 바탕으로 이를 잘 표현할 수 있는 선형 함수 $y = h(x) = w_{1} x + w_{2}$를 찾고자 하는 것이다. 이러한 함수를 찾으면 그 후에 예측하고자 하는 학습 시간이 입력되었을 때, 함숫값을 통해 예측을 생성한다.
위와 같은 선형 함수에 따르면 학습 시간이 약 10시간일 때, 예상되는 성적은 약 48점이다. 이처럼 함숫값을 찾아서 데이터에 주어지지 않은 학습 시간에 대해 성적을 예측할 수 있다.
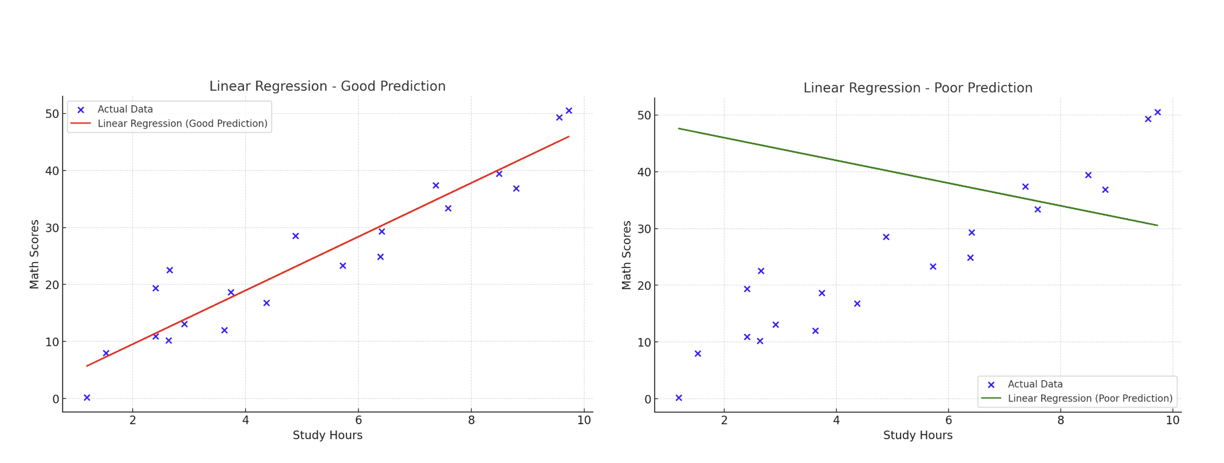
위 두 선형 회귀 결과를 비교해보았을 때, 어느 직선이 데이터를 더 잘 대변하는가? 좌측 plot이 더 산점도를 잘 표현하고 있음을 육안으로 확인 가능하다. 그렇다면 과연 데이터를 잘 대변(표현)하는 직선을 어떻게 찾을 수 있을까? 직선이 데이터를 잘 대변한다는 것은 어떤 기준으로 확인 가능할까?
How to Work - Gradient Descent
선형 회귀의 목적은 데이터를 잘 표현하는 직선을 찾는 것이고, 직선이 데이터를 잘 표현하기 위한 기준을 설정하여 선형 함수의 파라미터 $w_{1}, w_{2}$를 찾아야 한다.
이를 위해 직선이 데이터를 얼마나 잘 표현하는지를 판단하는 기준인 '손실 함수(Loss Function)'을 사용한다.
손실함수는 가설 함수 h(x)에 대해 다음과 같이 표현된다.
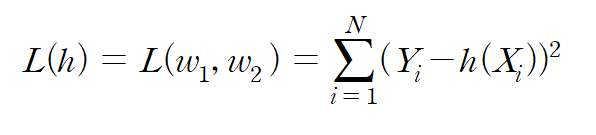
각 데이터 포인트에 대해 실제 값($Y_{i}$, target variable)과 가설 함수를 통한 예측 값($h(X_{i})$, prediction)의 차이를 구하고 이를 제곱한다. 이는 오차(error)의 제곱이라고 할 수 있다. 즉, 해당 손실함수는 각 데이터 포인트에 대한 오차의 제곱 합이라고 할 수 있다.(이를 Mean Square Errors, MSE라고 부른다)
만약 가설 함수가 이상적으로 모든 데이터 포인트를 정확히 예측할 수 있다면, 임의의 데이터 포인트에 대해 error가 0이므로 손실 함수가 0이다. 또한 손실함수가 0 이상이므로, 손실함수가 작을수록 선형 함수가 데이터를 잘 표현한다고 할 수 있다.
그렇다면 손실함수를 최소화하는 인자 $w_{1}, w_{2}$를 구하는 방법을 고민해야 한다. 먼저 손실 함수 식은 다음과 같이 나타난다.
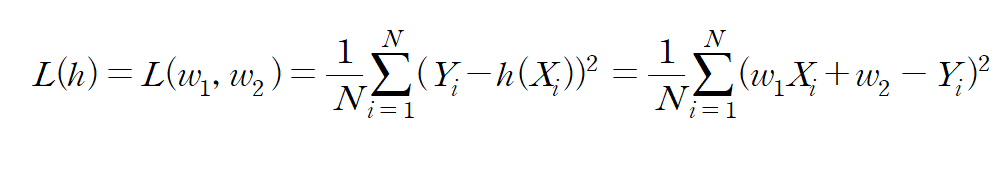
이를 구하는 방법으로 경사하강법(Gradient Descent)이 있다. 벡터 미적분학에 따르면 특정 점 X에서의 벡터 함수의 gradient는 해당 함수를 최대화하는 방향 벡터와 평행하다. 따라서 gradient의 음의 방향은 벡터 함숫값을 최소화하는 방향을 향하고 있기 때문에, 다음의 과정을 반복하여 함수를 local minimum으로 수렴하게 할 수 있다.
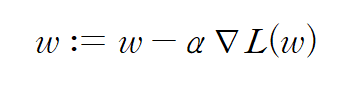
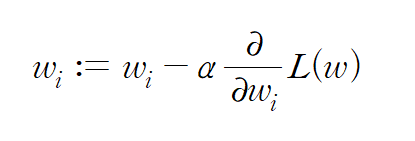
간단하게 말하면 아래로 볼록한 이차함수 위 한 점에서 미분계수를 생각해보라. 미분계수가 양수라면 x축의 음의 방향으로 점을 이동시키고, 미분계수가 음수라면 x축의 양의 방향으로 점을 이동시키자. 그럼 그 점은 극솟점에 가까워질 것이다. 미분계수의 절댓값이 크면 클수록 극점에서 먼 것이므로 미분계수의 크기에 비례하여 점을 이동시키는 것이 합리적일 것이다. 위 아이디어가 고안된 배경이다.
즉, 파라미터 w에 대해 위 과정을 반복하며 값을 업데이트하면 수렴하는 w는 함수 L을 최소화하는 파라미터가 된다.
따라서 선형회귀 함수 식 $h(X) = w_{1} X + w_{2}$에 대해 위 업데이트를 반복하여 계산하면(수렴할 때까지) 우리가 원하는 fitting line을 얻을 수 있다.
예시 문제 풀어보기
다음 주어진 데이터에 대해 최적의 fitting line y = ax + b를 구하시오.
| X : Time (hour, staying at home) | Y : Time (hour, playing the game) |
| 3 | 1 |
| 5 | 1.2 |
| 6 | 2 |
| 10 | 2.5 |
| 12 | 3 |
(sol)
최적의 fitting line은 손실함수를 최소화하는 함수이다. 또한 손실함수는 예측값과 실제값 차의 제곱의 합으로 구성된다.
|
1
2
3
4
|
import numpy as np
X = np.array([3, 5, 6, 10, 12]).reshape(-1, 1) # (5, 1)
Y = np.array([1, 1.2, 2, 2.5, 3]).reshape(-1, 1) # (5, 1)
|
cs |
손실함수를 정의한다.
|
1
2
3
4
5
6
7
8
9
10
11
|
def loss_function(X, Y, a, b):
return np.sum((Y - a*X - b)**2)
'''
(a*X + b - Y)^2을
a에 대해 미분하면 2(a*X + b - Y) * X
b에 대해 미분하면 2(a*X + b - Y)
'''
def derivative_loss(X, Y, a, b):
da = 2 * np.mean((a*X + b - Y) * X) # 성분 별 곱셈, 행렬곱 아님!
db = 2 * np.mean(a*X + b - Y)
return da, db
|
cs |
이제 학습을 진행한다. 미분계수 앞에 붙는 상수는 학습률(learning rate)이라고 부른다. 보통 $10^{-3}$ 정도의 값을 사용하며, 이 문제는 간단하므로 크게 잡아도 된다. 학습률을 바꿔보며 10 epoch(반복횟수의 단위)마다 출력되는 손실 함수의 값을 확인해보면 좋다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
import matplotlib.pyplot as plt
a, b = 0, 0
learning_rate = 0.01
for i in range(100):
da, db = derivative_loss(X, Y, a, b)
a = a - learning_rate * da
b = b - learning_rate * db
if i % 10 == 0:
print("Epoch %d, Loss Function : %f "%(i, loss_function(X, Y, a, b)))
plt.scatter(X, Y)
plt.plot(X, a*X + b)
plt.grid()
plt.show()
|
cs |

결과를 보면, 직선이 잘 fitting된 것을 확인 가능하다. 이 때 직선은 y = 0.247355 x + 0.120902이다.
Mulitiple Linear Regression
다중 선형 회귀는 변수가 2개 이상일 때 사용하는 선형 회귀 방법이다. attribute variable이 1개인 경우에는 가설 함수가 $ h(X) = w_{1} X + w_{2} $로 표현되었다. attribute variable이 2개 이상인 경우에는 식을 다음과 같이 적을 수 있다.
$ h(x_{1}, x_{2}, ..., x_{m}) = w_{0} + w_{1} x_{1} + w_{2} x_{2} + ... + w_{m} x_{m} $
(단, $w_{0}$은 절편)
이러한 가설함수에 대해 최적의 파라미터를 찾는 방법 또한 경사하강법을 이용해서 각각의 가중치 $w_{i}$를 업데이터하면 된다. 또한 이러한 식을 행렬과 벡터로 표현하면 더욱 간단하게 나타낼 수 있다.

따라서 구현 과정에서는 다음과 같이 행렬로 구현할 수 있다. 데이터를 살펴보면, 상수항을 표현하기 위해 데이터 포인트의 특성으로 1을 놓은 것을 확인할 수 있다. 이는 행렬곱 과정에서 $w_{0}$을 나타낸다. 행렬곱을 시행하면 그 결과가 column vector로 나타날 것이고, 이는 Y 벡터와 동일한 shape이므로 뺄셈 연산이 수행 가능하여 error를 계산할 수 있다.
Implementation

해당 데이터를 가지고 구현을 수행해볼 것이다. 데이터셋은 위와 같이 구성되어 있고, 회귀 분석을 위해 다음과 같이 문제를 정의한다.(본 데이터는 실제 데이터가 아닌, 임의로 생성한 데이터이다.)
age, weight, underlying disease, heart disease를 attribute variable로, heart rate를 target variable로 하는 회귀 분석
이를 해결하기 위해 데이터셋을 구성한다. 구성은 아래 코드와 같다.
import numpy as np
# 첫번째 열의 1은 w0를 위한 상수
X = np.array([ [1, 35, 50.1, 0, 0],
[1, 24, 73.5, 1, 1],
[1, 29, 55.4, 1, 0],
[1, 17, 61.8, 0, 0],
[1, 51, 87.0, 1, 1],
[1, 33, 45.4, 0, 0]])
Y = np.array([141, 110, 123, 108, 193, 153]).reshape(-1, 1)
# w0, w1, w2, w3, w4
W = np.array([0, 0, 0, 0, 0]).reshape(-1, 1)
그 다음은 가설함수와 손실함수에 대한 구현이다.
def hypothesis_function(X, W):
return np.dot(X, W)
def loss_function(X, W, Y):
Y_pred = hypothesis_function(X, W)
return np.mean((Y - Y_pred) ** 2)
또한 경사하강법을 위한 업데이트 식을 전개하고 이를 구현할 것이다.

def train(X, W, Y, epoch = 100000, alpha = 1e-5):
for e in range(epoch):
L = loss_function(X, W, Y)
if (e+1) % 100 == 0:
print("=== Epoch %d : Loss : %f ==="%(e+1, L))
# dL / dW를 구현
dL = np.dot((hypothesis_function(X, W)-Y).reshape(1, -1), X)
dL = dL.reshape(-1, 1) * 2
# 가중치 업데이트
W = W - alpha * dL
train(X, W, Y)
반복하는 학습 횟수를 epoch라고 부르고, 가중치 업데이트에 사용되는 계수를 learning rate(학습률, alpha)라고 한다. 학습률이 크면 학습이 빠르지만 loss function이 발산할 위험이 있고, 학습률이 작으면 학습 속도가 느리지만 안정적인 학습이 가능하다. 일반적으로는 learning rate로 $10^{-3}$정도를 사용하며, 위 데이터의 경우, $10^{-5}$일 때 안정적이다.
학습률을 늘려보면 gradient exploding(기울기 폭발)을 관찰 가능하다.

학습 횟수(/100회)에 따른 loss function의 값을 보면 점점 감소한다는 것을 확인 가능하다. 또한 10만 번 학습한 후, 모델의 예측을 보면 다음과 같다.
| # of Data Point | 실제 heart rate(Y) | prediction(Y_pred) |
| 1 | 141 | 150.19 |
| 2 | 110 | 108.18 |
| 3 | 123 | 122.88 |
| 4 | 108 | 108.47 |
| 5 | 193 | 195.35 |
| 6 | 153 | 140.80 |
즉, 초기 가중치가 모두 0이었던 점을 고려하면, 예측값이 실제값에 가깝게 갱신된 것을 확인할 수 있다.
또한 각 특성에 대해 업데이트된 가중치 벡터를 구해보면 $w_{0} = 11.4, w_{1} = 2.8, w_{2} = 0.79, w_{3} = -14.5, w_{4} = -14.8$임을 확인 가능하다. 즉, 학습을 통해 얻은 가설 함수 식이
$ h(X) = 11.4 + 2.8x_{1} + 0.79x_{2} - 14.5x_{3} - 14.8x_{4} $이다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [Machine Learning] 1. 데이터의 분석 : 데이터 전처리 (0) | 2025.01.04 |
|---|---|
| [Machine Learning] 0. 머신러닝이란? (3) | 2025.01.03 |